Математическое моделирование случайных событий в пошаговых стратегиях

Представьте себе мир, где каждый ваш ход в любимой пошаговой стратегии, будь то грандиозная битва за королевство или захватывающая космическая экспедиция, подчиняется не капризу случая, а предсказуемым закономерностям. Звучит невероятно? На самом деле, Математическое моделирование случайных событий в пошаговых стратегиях позволяет приблизиться к такому пониманию, отбросив завесу случайности и позволив игроку взглянуть на игру с совершенно новой, более аналитической точки зрения. Это не просто игра в числа – это глубокое погружение в мир вероятностей, статистики и математического анализа, способное не только улучшить ваши игровые навыки, но и открыть перед вами увлекательный мир математического моделирования.

Вероятностные процессы в игровом дизайне

Разработчики пошаговых стратегий активно используют случайные события для создания динамичной и непредсказуемой игровой среды. Бросок кубика, шанс критического удара, неожиданное появление вражеского подкрепления – все это элементы, добавляющие игре остроты и сложности. Однако, за внешней случайностью скрывается тщательно продуманная система вероятностных процессов. Понимание этих процессов – ключ к успеху. Изучая вероятность различных исходов, игрок может оптимизировать свои стратегии, предвидеть потенциальные риски и максимизировать свои шансы на победу.

Моделирование случайных величин

Сердцем математического моделирования в данном контексте является работа со случайными величинами. Это могут быть дискретные величины, такие как количество очков, выпавших на кубике, или непрерывные, например, урон, наносимый атакой. Для каждой такой величины можно построить математическую модель, описывающую ее распределение вероятностей. Это позволит игроку оценить среднее значение, дисперсию и другие характеристики случайной величины, чтобы принимать более обоснованные решения.

Применение теории вероятностей

Теория вероятностей играет ключевую роль в анализе игровых ситуаций. Используя различные теоремы и формулы, можно рассчитать вероятность различных исходов, например, вероятность победы в сражении при определенных условиях, вероятность успешного завершения миссии или вероятность получения определенного ресурса. Такой анализ позволяет игроку оценить риски и выгоды различных стратегий и выбрать наиболее эффективную.

Статистический анализ игровых данных

Математическое моделирование не ограничивается только теоретическими расчетами. Важную роль играет статистический анализ игровых данных. Записывая результаты своих игр, игрок может собрать статистическую информацию, которая поможет ему лучше понять поведение случайных событий в игре. Анализ этой информации позволит ему выявить закономерности, которые не были очевидны на первый взгляд, и скорректировать свою стратегию.

Сбор и обработка данных

Для эффективного статистического анализа необходим тщательный сбор и обработка данных. Важно фиксировать все значимые события в игре, такие как результаты сражений, количество полученных ресурсов, урон, нанесенный и полученный, и другие параметры. После сбора данных их нужно обработать, чтобы получить результаты, пригодные для анализа.

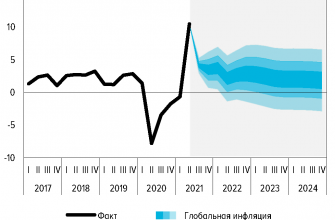
Визуализация данных

Графическое представление данных – важный инструмент для понимания сложных статистических закономерностей. Графики, гистограммы и другие визуальные средства позволяют быстро оценить распределение вероятностей, выбросы и другие особенности данных. Это помогает увидеть скрытые взаимосвязи и принять более взвешенные решения.

Практическое применение моделирования

Математическое моделирование случайных событий не только интересно с теоретической точки зрения, но и имеет практическое значение для улучшения игрового процесса. Понимание вероятностных закономерностей позволяет игроку разрабатывать более эффективные стратегии, минимизировать риски и максимизировать свои шансы на победу.

Оптимизация стратегий

Анализ вероятностей различных исходов позволяет игроку выбирать оптимальные стратегии в зависимости от текущей ситуации. Например, если вероятность победы в лобовом столкновении низка, то можно применить тактику обхода или засады. Понимание вероятностей помогает принимать более рациональные решения.

Управление ресурсами

Знание вероятности получения различных ресурсов позволяет игроку более эффективно управлять своими запасами. Можно предвидеть нехватку ресурсов и своевременно принять меры для их добычи или сохранения.

Оценка рисков

Математическое моделирование позволяет более точно оценить риски, связанные с различными действиями. Например, можно рассчитать вероятность потери важных юнитов в сражении и принять решение о необходимости избегать риска.

Стратегия	Вероятность успеха	Риск
Атака	60%	Высокий
Оборона	80%	Низкий
Отступление	90%	Минимальный

Данная таблица иллюстрирует как можно использовать математическое моделирование для оценки рисков и выбора стратегий.

Приглашаем вас ознакомиться с другими нашими статьями, посвященными миру математики и игрового дизайна!

Облако тегов

Вероятность	Стратегии	Моделирование
Статистика	Игры	Математика
Анализ	Риск	Данные